Navigation: This page 'spatial.html' --> aspects ---> Main Page. HELP. Contact. Admin.

The Spatial Aspect

Briefly ...

We experience the spatial aspect directly and intuitively as here, there, between, around, inside and outside. Spatial properties include shape, position, size, angle, orientation, proximity, surrounding, overlap, and so on. Things that gain their meaning from the spatial aspect include particular shapes (triangle, line, spiral, etc.), angles, distances, holes, space, area, dimension and so on. Like quantitative functioning, spatial functioning feels to us like a static property. A wiggly line is spatial, but if we call it a 'path', then we are importing some kinematic meaning of 'going'. Dooyeweerd's discussion of the spatial aspect is, unfortunately, all over the place and interwoven with discussion of its relationship with other aspects [NC:II, 63-65,85-96,98-106].

The good possibility that the spatial aspect introduces into temporal reality, which have no meaning in the quantitative aspect, are simultaneity and continuity. A quantitative thing in temporal reality, such as a set, can never exhibit two different amounts (e.g. 6 and 7) simultaneously, but a spatial thing, such as a triangle, is both here and there simultaneously since it extends from here to there and over all in between. If it did not, the triangle would be incomplete. The extension from here to there is continuous, not in discrete steps.

It is this that makes so-called irrational number(nesse)s like the square-root of 2 meaningful: as amounts, they cannot be arrived at by application of quantitative laws. In this we see the quantitative aspect antecipating the spatial, in that some amounts cannot be discovered except by antecipating spatial meaningfulness (e.g. 'square'). An example of retrocipation from spatial to quantitative is length: a spatial property that also obeys quantitative laws.

Defining the Aspect x

Kernel x

"Continuous extension" (Dooyeweerd's rendering)
"Here, there, between, around; inside and outside. Introduces Simultaneity, continuity" (Basden's intuitive rendering)
Spreading out in a continuous manner; see below
Simultaneity (in that its parts are all present simultaneously).

rather than:

Shapes
Occupying space (which is physical)
x,y coordinates (which are numerical)

Note: The kernel meaning of the spatial aspect needs to be as true for one-dimensional space as for two- and three-dimensional.

Some central themes x

dimension
size, position, slope, volume, shape, etc.
here, there, near, far, etc.
lines, areas, volumes, etc.
symmetry, overlapping, surrounding, etc.

Common Misconceptions x

Topology is spatial but can sometimes be more analytic than spatial when it involves having distinguished certain entities and their relationships, and then examining connectedness. Spatial here is more to do with the continuous extension in three (or two or four) dimensions. However, we might say that topology involves an analogy between the spatial and the analytical aspects.
Fourth dimension is not Time. While it is convenient to consider it a 'dimension' in terms of 'something that cannot be reduced to the other dimensions' as we do in physics, time as such is something completely different (see Time). Distinguishing different things so that we can more clearly think about them (which is what physicists are doing there) is analytical, even though they use the spatial term 'dimension' for what they do. What they are doing is to express both spatial dimensions and time as quantity - which is expressing both in quantitative terms, rather than treating them as space and time. While there is much power in doing this, this Dooyeweerdian approach would suggest that this is still just an analogy, not the real thing.
"The spatial is not in the least supra-temporal since it implies simultaneity in the modal meaning of continuous dimensional extension, and the spatial relations in temporal reality have subjective-objective duration of time. So far as the spatial relationships in abstract geometry are viewed apart from transitory things and events, i.e. according to their modal structure alone, they, nevertheless, always continue to express the spatial temporal order of greater and less in simultaneity." [NC,I:31 footnote, italics in original]

The Aspect Itself

Non-Absoluteness x

Special Science x

Geometry?
Geography (see below)
Study of spatial properties such as shape, orientatino, overlap, occlusion
Topology to some extent

Things and Institutions Qualified by the Spatial Aspect x

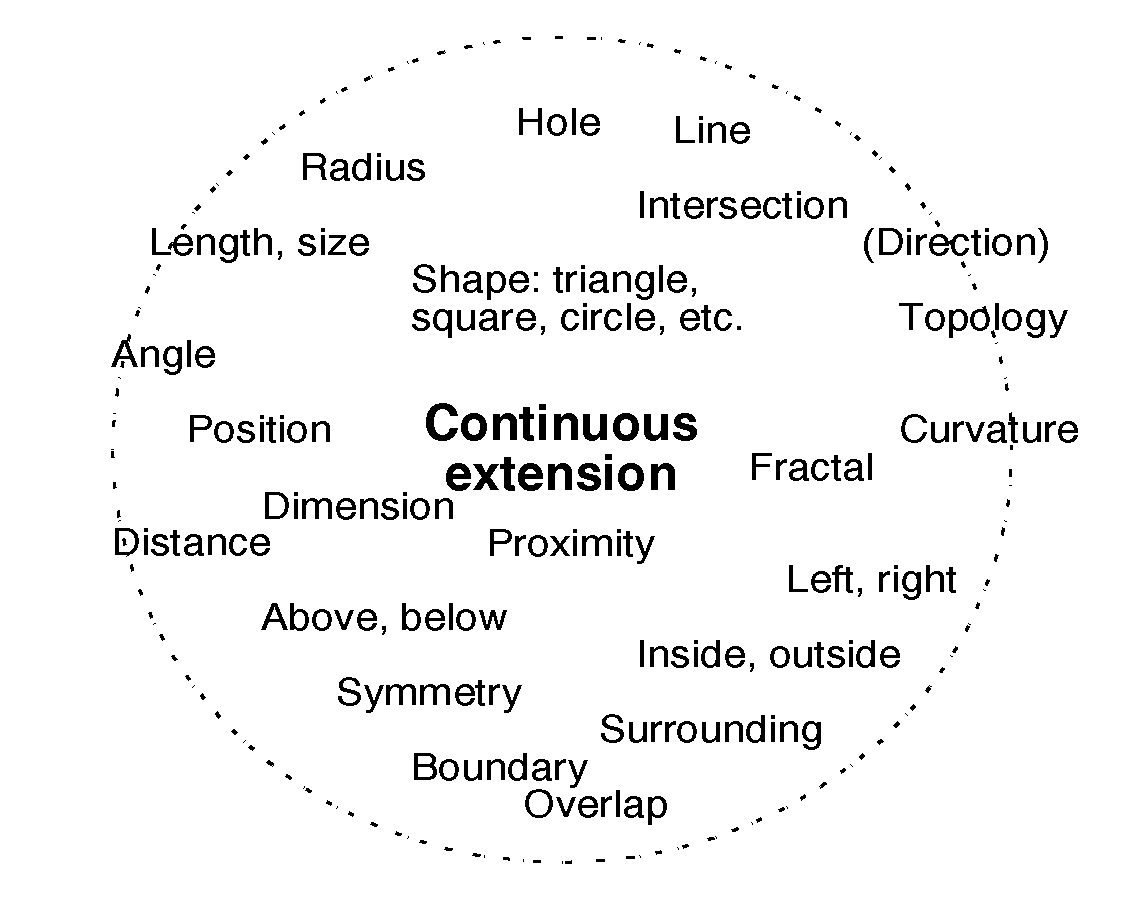
The spatial aspect and some of its constellation

Other things:

Sides, Edges, Corners
Holes (How many holes does a drinking straw have?)
Curves
Shapes
Areas, volumes
===== list to be compiled

Shalom x

Continuousness (in contrast to the discreteness of the quantitative aspect)
Extension

Harm x

Contributions from the Field x

The Aspect Among Others

Law-dependencies x

Number of dimensions is quantitative
Irreducibility to quantitative aspect? For example, is not position fully expressed as a tuple of numbers, and is not shape reducible to the number of sides it has? For the latter, no! Some shapes have curved boundaries, from oval to curved-cornered things, and these cannot be said to have a particular number of sides. Moreover, some shapes have no clear boundary, such as clouds exhibit. Dooyeweerd was insightful in making continuous extension the kernel meaning of the spatial aspect.

Analogies x

Position, length, size, etc. retrocipate quantitative amount - but they are not themselves quantitative.
Spatial simultaneity might have an analogy in the quantitative aspect in the factors in a number. The number is simultaneous with its various factors (whether multiplicative or additive) - but whereas spatial simultaneity is necessary (e.g. the triangle needs its three sides), in the quantitative it seems not necessary but almost merely derivative. Hence Goldbach's conjecture, that every even number is the sum of two primes.
Topology. Toplogy, the structure of the shape of a thing, that is invariant when the thing is stretched, seems to be spatial yet might involve two analogies. One is with the kinematic aspect, in that the stretching involves movement. The other is with the analytical aspect, in that topology also involves distinguishing certain 'parts' of the thing, notably holes. Distinguishing parts is a product of functioning in the analytical aspect. Thus toplogy is probably an analogy between the three aspects.
In line of sight spatial anticipates the sensitive aspect.
Affordances (Gibson, 1977). See Sensitive. A visual stimulus e.g. shape 'affords' certain representation ability. e.g. length or size of a shape more easily represents quantity rather than relationship. Thus spatial anticipates the lingual aspect.
Galadriel, in Tolkien's The Fellowship of the Ring, is offered the One Ring by Frodo.
"She lifted up her hand and from the rign that she wore there issued a great light that illumined her along and left all else dark. She stood before Frodo, now seeming tall beyond measurement, and beautiful beyond enduring, terrible and worshipful.
How come she was 'tall beyond measurement'? In Frodo's gaze she was not of infinite size. This 'tall beyond measurement' speaks of a spatial anticipation of something else, something pistic (to do with worship) probably.
"If people cannot walk out from the building onto balconies and terraces which look toward the outdoor space around the building, then neither they themselves nor the people outside have any medium which helps them feel the building and the larger public world are intertwined." (From Pattern 166 'The Gallery Surround' in Alexander's A Pattern Language.) Here the spatial anticipates the social aspect.

Antinomies x

Notes x

Hartshorne's Discussion

In a classic volume, The Nature Of Geography, Hartshorne discusses at some length what is the kernel of Geography. Is it:

An exact science? No.
The science of planet earth? No.
The study of landscape? No.
The study of relationship between natural environment and humankind? No.
The study of how humankind adapts to the natural environment? No.
The study of distributions on the earth's surface? No.

Rather, the kernel of Geography is:

The study of the areal differentiation of the earth's surface.

(Now we have access to other planets, presumably their surfaces would also be included in that.) "Differentiation" is the kernel of the analytical aspect, from which the central activity of science or close study comes. So what is being studied is areas - which is, in two dimensions, what Dooyeweerd proposed as the kernel of his spatial aspect.

Spreading Out & 'Continuous Extension'

We call the kernel meaning 'spreading out'. But Dooyeweerd suggested the kernel was 'continuous extension'. We replace that with 'spreading out', because I have found that 'continuous extension' can be misleading, referring for example to how projects continuously extend their deadlines and costs!

The more important question, however, is why the kernel is either of these (continuous extension or spreading out) rather than, for instance, position, length, shape, etc.? A recent discussion I had with a mathematician about might throw some light on this - there is something fundamentally different about continuous numbers ('reals') and integers.

Comments Received x

This is part of The Dooyeweerd Pages, which explain, explore and discuss Dooyeweerd's interesting philosophy. Questions or comments would be welcome.

Written on the Amiga with Protext.

Created: by 31 March 1998. Last modified: 30 August 1998 rearranged and tidied. 7 February 2001 copyright, email. 4 February 2002 spatial anticipation of the pistic in Tolkien's Galadriel. 21 January 2003 Spatial anticipating social in Alexander. 24 August 2005 brought up to date with .nav,.end, some rewriting of start. 30 January 2006 quotation from NC,I:31, rid counter. 27 February 2007 Curved and fuzzy shapes. 14 October 2008 simultaneity and 'true of 1D'. 17 July 2009 'spreading out'. 14 June 2010 line of sight. 22 September 2010 Dooyeweerd's and Basden's kernels. 21 September 2016 briefly. 26 September 2020 added constellation pic, corner, edge; Hdg= Things and Institutions Qualified by the Spatial Aspect. 2 January 2021 analogy of simultaneity in quantitative aspect. 22 September 2021 list of things. 20 January 2022 symmetry etc.