Navigation: This page 'www.dooy.info/anticipation.html' ---> Main Page. HELP. Contact. About Page.

Inter-Aspect Anticipations

It is sometimes difficult, especially for the newcomer, to decide what is of which aspect, since so many things seem to be borderling. Part of the reason for this is that each aspect anticipates those later than it, and many things in our experience are meaningful in both aspects. Also, each aspect retrocipates those earlier than it.

In anticipation, an aspect is "directed and animated" by later ones [NC II:153]. Yet, at the same time the anticipated aspect cannot be predicted or deduced solely from within the anticipating aspect alone. A nice statement of this is in fact found in another author, Michael Polanyi:

"Just as arithmetic is not logically rich enough for us to deduce a calculus from it, and words are not rich enough for us to deduce a grammar from them, so the laws of physics and chemistry would now be understood to be not rich enough for us to deduce the characteristics of sentience from them, and we should cease trying to do so." [Polanyi & Prosch, Meaning, 1975, 178]

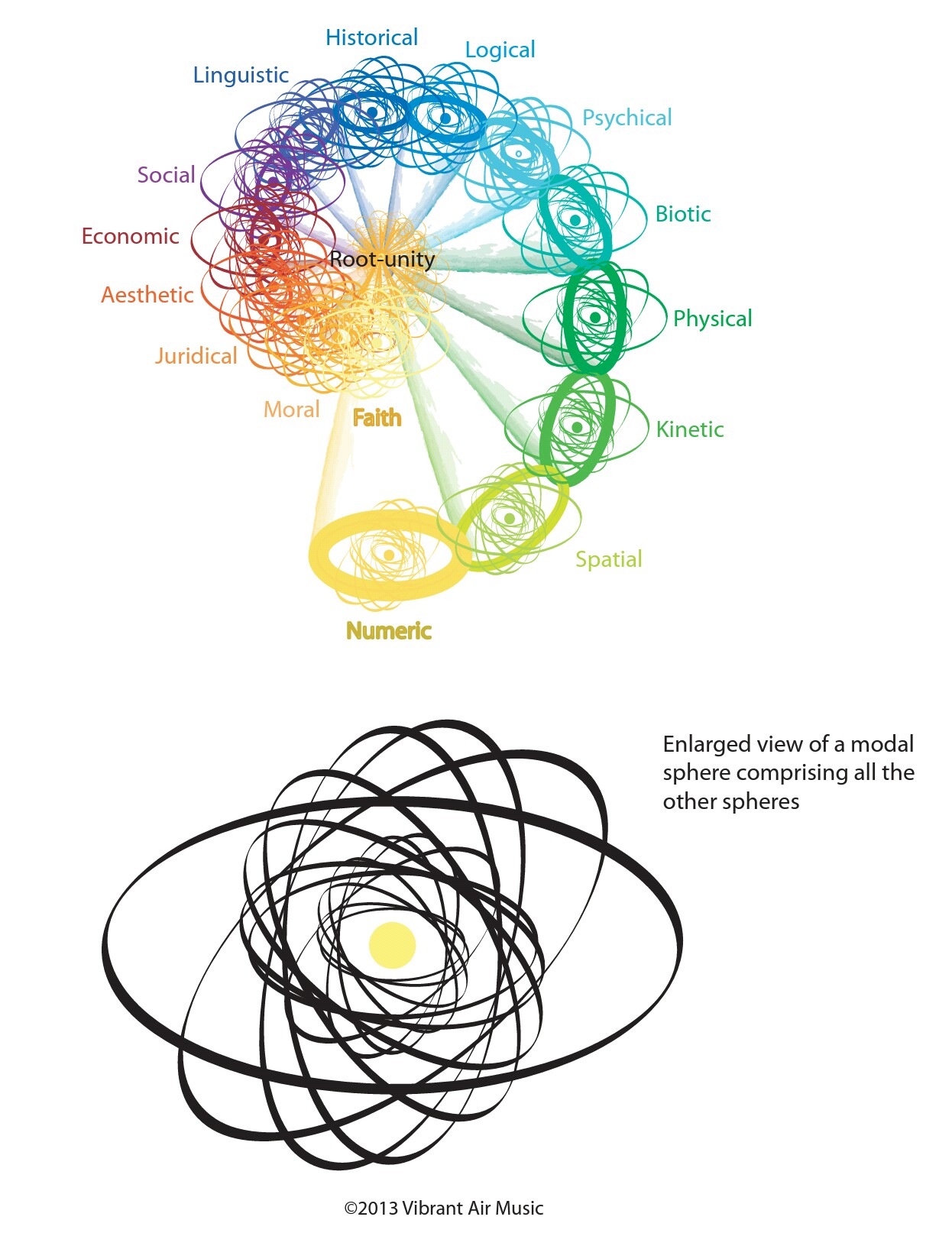
The following diagram (created by Janet Danielson, used with permission) illustrates the intertwinement of the aspects. Each aspect has echoes of all the others and each builds on or anticipates all the others.

Understanding the nature of anticipation can help us identify the important aspects of things.

Anticipation is of two types: dependency and analogy. Dependency in the anticipatory direction is when something in an aspect is there 'for the purposes of' the later aspect, and, unless the meaning of that later aspect is taken into account, feels arbitrary and is little more than a curiosity in its own aspect. Analogy (which can be either anticipatory or retrocipatory) is a non-dependency similarity, an 'echo', of one aspect in another; for example, logical entailment echoes causality. Dependency entails necessity or meaningfulness; analogy does not. In this page we deal mainly with dependency.

On the difference between anticipation and retrocipation: They are in opposite directions but they are not quite the converse of each other. If we have two aspects X and Y, where X precedes Y, then X anticipates Y if this is governed by the laws of X, but Y retrocipates X if it is governed by the laws of Y. For example, economy of thought is analytical aspect antecipating economic insofar as it is governed by the laws of the analytical aspect, nott the economic [NC,II, 122]. However, if we treat thoughts as a resource (as perhaps in Knowledge Management) this might be an economic retrocipation of the logical.

First, we briefly discuss two examples of how a couple of aspects anticipate some of the aspects later than them - the physical and the quantitative.
That an aspect anticipates the next one is particularly important in the functioning of the latter, so we give a table of Next-Aspect Anticipations first.
This is followed by a table of how the quantitative aspect might anticipate nearly every later aspect, to illustrate various ways in which we might tease our the issue that is anticipation.
Finally, we bring together some guidelines for our investigation of anticipations.

An Example from the Physical Aspect

From the point of view of the physical aspect we think of atoms, molecules, chemicals, materials, and the forces etc. that affect them. Keeping our thinking within the physical aspect, we can produce what chemists call inorganic chemicals and materials, such as minerals, metals, etc. We might stumble upon what they call organic materials - those based on carbon chemistry - but would not think of them as special in any way. Rather, we would think of the long molecular chains of carbon and hydrogen (that are the basis of organic materials) as rather uninteresting and also rather fragile, when compared with much more diverse materials that involve the other 90 elements. We would be much more fascinated with the properties of gold, iron, uranium, calcium, and the like, with the differences between solids, liquids, gases and plasmas, etc. Organic chemicals, materials would have little meaning to us.

But the meaning of organic chemistry - its importance, its interestingness - becomes apparent when we think from the point of view of the biotic aspect of life. It is organic materials of which living things are composed, and which possess the special properties that allow life to occur.

Those physical-chemical-material properties are not life themselves - because the notion of 'life' has no meaning from the physical aspect - but rather they are the very properties that support and implement what, from the point of view of the biotic aspect, we would call life.

That is, the physical aspect anticipates the biotic. They anticipate the biotic life functions. The life-supporting physical phenomena are there all the time, but they have no special meaning from the point of view of the physical aspect. Rather, their meaning, their special significance, lies in the biotic aspect.

An Example from Number

The quantitative aspect is to do with quantity, with amount, with countability. Imagine yourself as a thinker about amount. From countability you gain the notion of integers and fractions - the 'rational' numbers, so called because they can always be expressed as a ratio of two integers - and you eventually notice that, given any two rationals, no matter how close together, you can always find another rational between them. Every number (quantity) that you come across seems to be separated from its neighbour by a 'gap'; numbers are discrete.

You might wonder whether one could ever obtain a situation in which the numbers merged with each other continuously, but, if you stayed with countability, you would never discover continuous number, nor would you even find a need for them. You might speculate about them, argue whether they 'exist' or not, but (as long as you did not make reference to meaning from other aspects) they would remain at best meaningless curiosities.

But if you start to think about space rather than amount and countability - that is start to think from the point of view of the spatial aspect whose kernel meaning is continuous extension - then you would start to find a need for continuous number and encounter what mathematicians call irrational numbers - numbers that cannot be expressed perfectly as a ratio of two integers. Pi is a well known example. Then, as you use number to express spatial phenomena - via graphs, trigonometry, etc. - you start to see number as continuous rather than discrete. In fact, after a time - at least so I found - the continuity of number became such an ingrained assumption that it seems artificial to think of number as fundamentally discrete.

Neither continuous number nor the need for it can never be discovered if our thinking stays within the realms of the quantitative aspect. But it seems such numbers lurk there nevertheless, waiting to be discovered when we move our thinking to the spatial aspect.

This is one way in which the quantitative aspect anticipates the spatial: the continuity of number has no meaning from within the former, but only within the latter aspect.

Anticipating the Next Aspect

This suggests things in each aspect that anticipate the next. That is, they are things of the given aspect but, until the meaning of the next is taken into account, they remain of little interest, and are little more then curiosities with certain properties. Currently, some of the entries are speculative, and I have yet to read in detail whether Dooyeweerd himself gave any examples. If you can think of better ones, please contact me. See also reflections on the affinities and differences between neighbouring aspects.

Aspect Kernel Of this
Aspect Anticipates
the Next

Quantitative Discrete amount Integers, ratios 'Irrational' numbers
(Discussed below)

Spatial Continuous extension Length, position, shape, orientation Direction, Changing position

Kinematic Flowing movement Animation, Mechanics

Physical Energy, mass Causality;
Atoms, Molecules, Chemicals, Materials Organic chemicals
(Discussed below)

Biotic Life functions;
Maintenance of Organism Respiration, Digestion, Repair, Reproduction;
Cells, Systems, Skin Autopoiesis;
Nerve cells and ability to respond

Sensitive Sensing and Feeling Hearing, Seeing, Remembering;
Signals, States Pattern detction

Analytical Distinction Figure-Ground separation, Pattern recognition, Cartesian Subject-Object separation;
Concepts, Theories Recognising similarities;
Linking of concepts

Formative Formative power Achieving, Shaping, Planning;
Goals, Structure, Skills Structuring of concepts for some end

Lingual Meaning carried by Symbols Semantic meaning, Writing, Speaking;
Topic or content of text, utterances Cultural connotations;
Linguistic Pragmatics

Social Social interaction Greeting, Deferring;
Social relationships, Institutions, Exchange

Economic Frugality Management, Production, Consumption;
Limits, Resources, Goods, Customers Parsimony

Aesthetic Harmony and Fun Resting, Playing, Harmonizing;
Music, Humour ?

Juridical Giving Each Their Due Appropriateness, Proportionality;
Responsibility, Rights, Legal systems Goodness (or Badness) of Law; "The notion of juridical guilt anticipates that of ethical guilt, and could not be understood without it." [Henderson:165].

Ethical Self-giving Agape-Loving, Giving of Oneself;
Generosity, Acts of Sacrifice, Repentance?, Forgiveness?;
A genuinely self-critical attitude.

Pistic Commitment Believing, Trusting;
Faith, Loyalty, Certainty (Ultimate commitment to what we take to be Divine)

Aspect	Kernel	Of this Aspect	Anticipates the Next
Quantitative	Discrete amount	Integers, ratios	'Irrational' numbers (Discussed below)
Spatial	Continuous extension	Length, position, shape, orientation	Direction, Changing position
Kinematic	Flowing movement	Animation,	Mechanics
Physical	Energy, mass	Causality; Atoms, Molecules, Chemicals, Materials	Organic chemicals (Discussed below)
Biotic	Life functions; Maintenance of Organism	Respiration, Digestion, Repair, Reproduction; Cells, Systems, Skin	Autopoiesis; Nerve cells and ability to respond
Sensitive	Sensing and Feeling	Hearing, Seeing, Remembering; Signals, States	Pattern detction
Analytical	Distinction	Figure-Ground separation, Pattern recognition, Cartesian Subject-Object separation; Concepts, Theories	Recognising similarities; Linking of concepts
Formative	Formative power	Achieving, Shaping, Planning; Goals, Structure, Skills	Structuring of concepts for some end
Lingual	Meaning carried by Symbols	Semantic meaning, Writing, Speaking; Topic or content of text, utterances	Cultural connotations; Linguistic Pragmatics
Social	Social interaction	Greeting, Deferring; Social relationships, Institutions,	Exchange
Economic	Frugality	Management, Production, Consumption; Limits, Resources, Goods, Customers	Parsimony
Aesthetic	Harmony and Fun	Resting, Playing, Harmonizing; Music, Humour	?
Juridical	Giving Each Their Due	Appropriateness, Proportionality; Responsibility, Rights, Legal systems	Goodness (or Badness) of Law; "The notion of juridical guilt anticipates that of ethical guilt, and could not be understood without it." [Henderson:165].
Ethical	Self-giving	Agape-Loving, Giving of Oneself; Generosity,	Acts of Sacrifice, Repentance?, Forgiveness?; A genuinely self-critical attitude.
Pistic	Commitment	Believing, Trusting; Faith, Loyalty, Certainty	(Ultimate commitment to what we take to be Divine)

How the Quantitative Aspect Anticipates All Others

Here we suggest how the quantitative aspect anticipates each of the later aspects. Its anticipation in later aspects is when something about quantity takes on meaning that is found only the later aspect. The 'something' might be the type of quantity itself (as in the case of irrationals) or what we do with the quantities (such as circular quantities found in the sensitive aspect below). The purpose of the following table is to show how we can tease out different ways of anticipating. Notice how anticipation is centred on the notion of meaningfulness.

To construct it we have tried to avoid simply 'slot-filling'. Rather, we have asked ourselves the very specific questions centred on meaningfulness:

"In what way is 'amount' or 'more, less' meaningful in this aspect? Is there any special, meaningful way in which amounts, more or less stand in relation to each other in this aspect? Is there any special, meaningful way in which amounts, more or less are manipulated that is required by this aspect?"

Aspect	Kernel	Types of quantity	How quantity is used
Quantitative	Discrete amount	Integers, Ratios, Unity (as oneness), Averages	Arithmetic operations, Statistics
Spatial	Continuous extension	Irrationals [NC, II:185]. (But not size nor number of dimensions; see note below.)	Approximation [NC, II:185], Raising to a powers (e.g. square, cube)
Kinematic	Flowing movement	Complex numbers [NC, II:170,172]. Negative numbers (movement in number). Infinitesimals.	Differentiation [NC, II:185],
Physical	Energy, mass	Basic physical constants?
Biotic	Life functions; Maintenance of Organism	Unity (the organism as itself and not another)	Fibonacci series? (much in evidence in living things) (but might this have meaning in the quantitative aspect without the biotic?)
Sensitive	Sensing and Feeling	Logarithms, e.g. decibels for sound level, levels of brightness perceived	Circular quantity, in which when we get to a certain amount we start again at zero, e.g. piano octaves, the colour circle Green - Cyan - Blue - Purple - Red - Orange - Yellow - Green ... (But we also find circularity in compass directions in the spatial aspect.)
Analytical	Distinction	Perhaps discreteness itself anticipates analytic distinction? (The usage of 0, 1 to represent TRUE and FALSE is mere symbolic convention, and not a true quantitative anticipation of the analytic aspect.)	Enumeration (integers used to identify distinct items, such as chapters in a book). Logical quantification?
Formative	Formative power	Dates. Numerical order: the direction of numeric sequence (See note below..
Lingual	Symbolic signification	Can anyone think of one? (Digits? I don't think so; that is symbols used to signify specifically quantitative meaning, not amounts that are of a special type that would remain a speculative curiosity until linguality is taken into account.)
Social	Social interaction
Economic	Frugality	Limits	Double-entry book keeping (in which as you increase one number you must always decrease another number by the same amount)
Aesthetic	Harmony, Fun, Interestingness	Problematic: there might be no genuine quantitative anticipation of the aesthetic because of the nature of the aesthetic aspect. We must avoid slot-filling. See note below. Maybe Factors? ("The same in the other") (but this is more like the aesthetic retrocipating the quantitative aspect, because factors have meaning within the quantitative aspect without reference to the aesthetic). Maybe numbers that are 'interesting' (e.g. primes) are those that anticipate the aesthetic? (But primes have meaning in the quantitative aspect without reference to the aesthetic.)	Likewise, there seems to be no special way in which we manipulate or relate amounts for aesthetic purposes.
Juridical	Giving Each Their Due	('Proportionality' would seem to have quantitative connotations, but when we look at its true juridical meaning, these connotations fade.)
Ethical	Self-giving
Pistic	Commitment	Infinity?

If you can think of better or more examples, please contact me.

Notes

1. Spatial aspect. Note the difference between true anticipatory dependency of the quantitative on the spatial in irrational numbers, and two other quantitative-spatial linkings. Number of dimenstions is how spatial depends foundationally on the quantitative. Size and length is an analogical rather than dependency relationship between spatial and quantitative.

2. Formative aspect. I believe, against Dooyeweerd, that numerical order anticipates the formative aspect, because without the latter there is no reason to place them in order; see fuller reasons.

3. Aesthetic aspect. Maybe there is no genuine quantitative anticipation of the aesthetic aspect. It is difficult to see how the aesthetic can be quantitative. While we might say "This music is more harmonious than that", it is very difficult to say what greater or lesser harmony is. Similarly "more funny". There seems to be no special type of amount, moreness or lessness that is specifically aesthetic, and for which we employ amount, moreness, lessness in a special way in relation to this aspect. I can think of no way of answering our core questions for the aesthetic aspect.

Guidelines for Anticipating Later Aspects

The overall rule is: Start with an idea of an anticipation, but then be critical of your idea. Do not merely fill slots and leave it at that.
Remember: Anticipation is based on meaningfulness, rather than on being or process or types. Ask yourself: to what extent is the link based on meaning? Therefore, we might ask ourselves the questions like the following (which we used in constructing the table of quantitative anticipations above) in which we substitute things meaningful within our aspect for amount, more or less.
- In what way are concepts like 'amount, more, less' meaningful in this aspect?
- Is there any special, meaningful way in which amounts, more or less stand in relation to each other in this aspect?
- Is there any special, meaningful way in which amounts, more or less are manipulated that is required by this aspect?
Is it anticipatory analogy or anticipatory dependency? In the latter, there is an element of meaninglessness in the thing of the earlier aspect until the (meaning of the) later aspect is taken into account. Ask yourself:
- If I ignore meaning from the later aspect, does this thing become nothing more than a curiosity? If so, then it is anticipatory dependency.
Is it really a foundational dependency in reverse? For example spatial number of dimensions depends foundationally on discrete quantity. This is usually an easy one to sort out. There is neither anticipation nor analogy here.
It is important to differentiate aspect X anticipating aspect Y from aspect Y retrocipating aspect X. It would seem (though it is not fully clear in Dooyeweerd) that the latter is not merely the former in the reverse direction. An example of each drawn from above:
- Anticipation: Irrational numbers anticipate the spatial meaning; they are mere speculative curiosities until we take spatial meaning into account.
- Retrocipation: Example: Spatial size retrocipates quantity. Example: The aesthetic notion of ('the same in the other' retrocipates quantitative factors (e.g. we find both 2 and 3 in 6). It is not an anticipatory dependency because factors are meaningful in the quantitative aspect without any reference to the aesthetic. So it is better to say it is a retrocipation.
Is it anticipation or functioning in an aspect? For example, digits? I don't believe this is a quantitative anticipation of the lingual, but rather the lingual functioning by which we use symbols to signify, in this case quantitative, meaning.

This page, "http://www.dooy.info/anticipation.html", is part of The Dooyeweerd Pages, which explain, explore and discuss Dooyeweerd's interesting philosophy. Questions or comments are very welcome.

Compiled by Andrew Basden. You may use this material subject to conditions.

Written on the Amiga with Protext.

Created: ? 16 Jan 2003. Last updated: 3 March 2003 .nav. 8 August 2003 Table of 'Next' anticipations, and list of later anticipations of quantitative aspect. 14 August 2003 self-critical attitude. 4 September 2003 feelings of justice. 11 October 2003 jur-eth, qv-kin anticipations from Henderson. 18 January 2005 corrected links. 25 May 2005 revamped; table of quantitative anticipations; Guidelines added. 19 March 2008 asp.neighbours. 14 June 2010 ant. as animating. 14 October 2013 Janet Danielson's lovely diagram. 15 June 2017 KarlHeintz said the fig missing; I found it and placed it in pix/; new .end,.nav. 28 November 2017 added quote from Polanyi. 17 November 2020 anticipation v retrocipation.